Регистрация Спросить otvet5GPT
filysh74
22.03.2021 16:09
Математика
Есть ответ 👍

Радиус каждой окружностм 2 см.узнай длину и ширину прямоугольника.сделай такой чертеж в тетради

145
484
Посмотреть ответы 2

Ответы на вопрос:

AльфаDog
AльфаDog
4,8(93 оценок)
Длина 2 см ширина 1см ну мне так кажется
matveizuikov
matveizuikov
4,6(46 оценок)

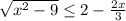
\sqrt{x^{2} -9} \leq 2-\frac{2x}{3}

ОДЗ :

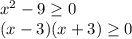
x^{2} -9 \geq 0\\(x-3)(x+3) \geq 0\\

x Є (-∞ ; -3] U [3 + ∞)

------------------------------

Рассмотри первый случай, когда правая часть >= 0 мы можем возвести обе части в квадрат :

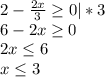
2-\frac{2x}{3} \geq 0 | *3\\6-2x \geq 0\\2x\leq 6\\x\leq 3

------------------

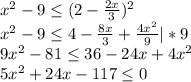
x^{2} -9 \leq (2-\frac{2x}{3} )^{2} \\x^{2} -9 \leq 4-\frac{8x}{3} +\frac{4x^{2} }{9} | *9\\9x^{2} - 81\leq 36 - 24x + 4x^{2} \\5x^{2} +24x-117 \leq 0

Приравняем левую часть к нулю, чтобы найти корни и разложить на множители:

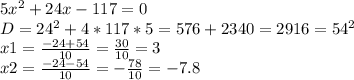
5x^{2} +24x-117 = 0\\D = 24^{2} +4*117 *5 =576 +2340 = 2916 = 54^{2} \\x1 = \frac{-24+54}{10} =\frac{30}{10} =3\\x2 = \frac{-24-54}{10} =-\frac{78}{10} =-7.8

Разложим на множители по формуле A(x-x1)(x-x2) :

5x^2+24x-117 = 5(x-3)(x+7.8)

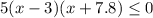
5(x-3)(x+7.8) \leq 0

Решим методом интервалов:

        +                        -                         +

---------------[-7.8]-----------------[3]---------------------

x Є [-7.8 ; 3]

Рассмотрим второй случай, когда правая часть меньше нуля :

Левая часть всегда больше либо равно 0, а если правая меньше нуля, то решений не существует, поскольку + всегда больше -, x Є ∅

Соединим все решения :

x Є [-7.8 ; 3] и x Є (-∞ ; -3] U [3 + ∞)

ответ : x Є [-7.8 ; -3] U {3}, у вас такого варианта нет, но у меня полностью правильный ответ

P.S можете сами подставить любое число, которое не входит в мой промежуток, но подходит для всех ваших вариантов, например -10

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS