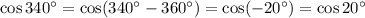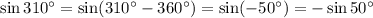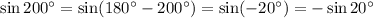Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Раскрой скобки: (x−2)⋅(x−9). (Пиши в каждое окошечко одно число или знак.)...
 lollo200311.12.2020 00:03
lollo200311.12.2020 00:03 -
Вычисли приближённое значение заданного числа по недостатку с точностью...
 AльфаDog26.06.2023 23:26
AльфаDog26.06.2023 23:26 -
Решите алгебра 8 класс...
 annakolupaewa2027.05.2021 14:49
annakolupaewa2027.05.2021 14:49 -
Первую половину пути поезд со скоростью 50 км/ч, а затем увеличил скорость....
 zalina5921.01.2020 12:47
zalina5921.01.2020 12:47 -
Решить систему сложения...
 allagureva23.07.2021 19:44
allagureva23.07.2021 19:44 -
Докажите: sina+cosπ/3=2sin(a/2+π/12)cos(a/2-π/12)...
 danilabelinovp08mj925.10.2022 16:52
danilabelinovp08mj925.10.2022 16:52 -
Рассчитать амортизационные отчисления для оборудования предприятия. Состав...
 АтинаАссорти09.04.2021 14:41
АтинаАссорти09.04.2021 14:41 -
ЗАРАНЕЕ ОГРОМНОЕ ТОЛЬКО 5 ОТМЕЧЕНЫХ НОМЕРОВ 3...
 Lilpump022827.02.2022 07:08
Lilpump022827.02.2022 07:08 -
На заводе при проверке на качество партии деталей в количестве 250 штук...
 niggaeasyreal22.02.2022 03:54
niggaeasyreal22.02.2022 03:54 -
Шахматист выигрывает партию с вероятностью 0,7. Найдите вероятность, что...
 GremMaster30.06.2022 08:55
GremMaster30.06.2022 08:55

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.


 или
или