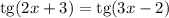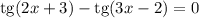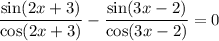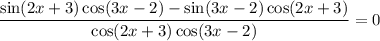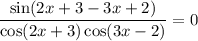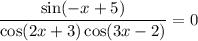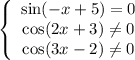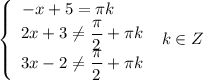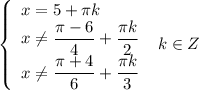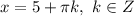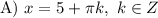Регистрация Спросить otvet5GPT
vasilzuk
16.01.2020 11:32
Математика
Есть ответ 👍

Зная что а> ,с< 0,сравните с 0 значение выражения а²с. а) а²с> 0 б) а²с< 0 в) а²с< 0 г) а²с=0

226
397
Посмотреть ответы 2

Ответы на вопрос:

ПрофессорДикинсон
ПрофессорДикинсон
4,6(77 оценок)
Зная что a> 0, a - положительное число знаем и что  a²> 0 , а²  - положительное число т.к. c< 0, с - отрицательное число умножение отрицательного и положительного числа мы получим отрицательное число. следовательно, ответ: б) a²c  < 0
clicker666
clicker666
4,4(48 оценок)

\text{tg} (2x + 3) = \text{tg} (3x - 2)

\text{tg} (2x + 3) - \text{tg} (3x - 2) = 0

\dfrac{\sin (2x + 3)}{\cos (2x + 3)} - \dfrac{\sin (3x - 2)}{\cos (3x - 2)} = 0

\dfrac{\sin (2x + 3)\cos(3x - 2) - \sin (3x - 2)\cos(2x + 3)}{\cos(2x + 3)\cos (3x - 2)} = 0

\dfrac{\sin (2x + 3 - 3x + 2)}{\cos(2x + 3)\cos (3x - 2)} = 0

\dfrac{\sin (-x + 5)}{\cos(2x + 3)\cos (3x - 2)} = 0

\left\{\begin{array}{ccc}\sin (-x + 5) = 0 \\\cos(2x + 3) \neq 0\\\cos(3x - 2) \neq 0\end{array}\right

\left\{\begin{array}{ccc}-x + 5 = \pi k \ \ \ \ \ \\2x + 3 \neq \dfrac{\pi}{2} + \pi k\\3x - 2 \neq \dfrac{\pi}{2} + \pi k\end{array}\right \ k \in Z

\left\{\begin{array}{ccc}x = 5 + \pi k \ \ \ \ \ \ \ \\x \neq \dfrac{\pi - 6}{4} + \dfrac{\pi k}{2} \\x \neq \dfrac{\pi + 4}{6} + \dfrac{\pi k}{3} \end{array}\right \ k \in Z

x = 5 + \pi k, \ k \in Z

ответ: \text{A}) \ x = 5 + \pi k, \ k \in Z

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS