Регистрация Спросить otvet5GPT
gromalex201
03.04.2020 04:13
Алгебра
Есть ответ 👍

Решите неравенство log с основой 3(x+2)< 1

162
332
Посмотреть ответы 2

Ответы на вопрос:

Yakubovadiana
Yakubovadiana
4,6(18 оценок)
Логарифмические уравненияуравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется  логарифмическим уравнением.простейшим логарифмическим уравнением является уравнение видаloga  x  =  b.(1)утверждение 1.  если  a  > 0,  a  ≠ 1, уравнение (1) при любом действительном  b  имеет единственное решение  x  =  ab.пример 1.  решить уравнения: a) log2  x  = 3,       b) log3  x  = -1,       c)  решение.  используя  утверждение 1, получим  a)  x  = 23  или  x  = 8;     b)  x  = 3-1  или  x  =  1/3;     c)    или  x  = 1. основные свойства логарифма.p1.  основное логарифмическое тождество: где  a  > 0,  a  ≠ 1 и  b  > 0.p2.  логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей: loga  n1·n2  = loga  n1  + loga  n2        (a  > 0,  a  ≠ 1,  n1  > 0,  n2  > 0).замечание.  если  n1·n2  > 0, тогда свойство  p2  примет видloga  n1·n2  = loga  |n1| + loga  |n2|       (a  > 0,  a  ≠ 1,  n1·n2  > 0).p3.  логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя        (a  > 0,  a  ≠ 1,  n1  > 0,  n2  > 0).замечание.  если  , (что равносильно  n1n2  > 0) тогда свойство  p3  примет вид        (a  > 0,  a  ≠ 1,  n1n2  > 0).p4.  логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа: loga  n  k  =  k  loga  n          (a  > 0,  a  ≠ 1,  n  > 0).замечание.  если  k  - четное число (k  = 2s), тоloga  n  2s  = 2s  loga  |n|       (a  > 0,  a  ≠ 1,  n  ≠ 0).p5.  формула перехода к другому основанию:         (a  > 0,  a  ≠ 1,  b  > 0,  b  ≠ 1,  n  > 0),в частности, если  n  =  b, получим        (a  > 0,  a  ≠ 1,  b  > 0,  b  ≠ )используя свойства  p4  и  p5, легко получить следующие свойства        (a  > 0,  a  ≠ 1,  b  > 0,  c  ≠ )            (a  > 0,  a  ≠ 1,  b  > 0,  c  ≠ )          (a  > 0,  a  ≠ 1,  b  > 0,  c  ≠ )и, если в (5)  c  - четное число (c  = 2n), имеет место          (b  > 0,  a  ≠ 0, |a| ≠ )перечислим и основные свойства логарифмической функции  f(x) = loga  x: область определения логарифмической функции есть множество положительных чисел.область значений логарифмической функции - множество действительных чисел.при  a  > 1 логарифмическая функция строго возрастает (0 <   x1  <   x2  þ  loga  x1  < loga  x2), а при 0 <   a  < 1, - строго убывает (0 <   x1  <   x2    þ  loga  x1  > loga  x2).loga  1 = 0 и loga  a  = 1     (a  > 0,  a  ≠ 1).если  a  > 1, то логарифмическая функция отрицательна при  x  î  (0; 1) и положительна при  x  î  (1; +¥), а если 0 <   a  < 1, то логарифмическая функция положительна при  x  î  (0; 1) и отрицательна при  x  î  (1; +¥).если  a  > 1, то логарифмическая функция выпукла вверх, а если  a  î  (0; 1) - выпукла вниз.следующие утверждения (см., например, [1]) используются при решении логарифмических уравнений.утверждение 2.  уравнение loga  f(x) = loga  g(x)     (a  > 0,  a  ≠ 1) равносильно одной из систем (очевидно, выбирается та система, неравенство которой решается проще)f(x) =  g(x),        f(x) =  g(x),f(x) > 0,g(x) > 0.утверждение 3.  уравнение logh(x)  f(x) = logh(x)  g(x) равносильно одной из системf(x) =  g(x),          f(x) =  g(x),h(x) > 0,h(x) > 0,h(x) ≠ 1,h(x) ≠ 1,f(x) > 0,g(x) > 0.
artyrik412002
artyrik412002
4,5(14 оценок)

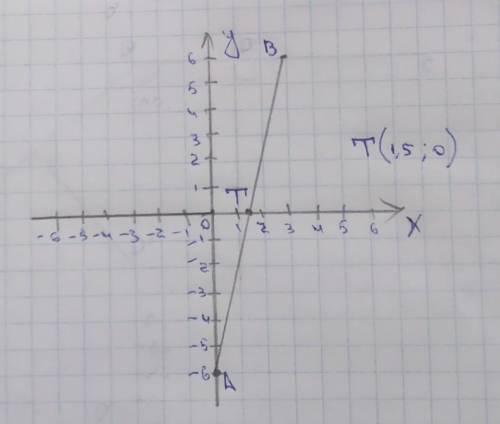
координаты середины отрезка АВ

Т(1,5; 0). ( если хочешь можешь поставить другую букву)


Найдите координаты середины отрезка АВ, если А(0;-6);В(3;6)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS