SaLmOn4663

19.08.2020 09:12

Геометрия

Есть ответ 👍

Решите , подробно ! 1. в равнобедренной трапеции сумма углов при большем основании равна 96°. найдите углы трапеции. 2. докажите, что параллелограмм, у которого соседние стороны равны, является ромбом. заранее и огромное ! 34

131

381

Посмотреть ответы 3

Ответы на вопрос:

babchykalinka

Геометрия

4,8(77 оценок)

1)сумма всех углов трапеции = 360 => сумма углов при меньшем основании = 360-96=264; трапеция равнобедренная => углы при большем основании равны, углы при нижнем основании равны => угол при большем основании = 96/2=48, а угол при меньшем основании = 264/2=132; 2) из определения ромба следует, что ромб - это параллелограмм у которого все стороны равны, а так как в параллелограмме соседние стороны равны, следовательно все стороны равны, и следовательно параллелограмм есть ромб

maritsumie

Геометрия

4,4(96 оценок)

1) сумма углов прилегающих к одной стороне трапеции равна 180 получается другой угол 180-96=84 также другой угол. получается 84; 84 2) ромб это фигура у которой все стороны равны и диагонали пересекаются пол прямым углом у параллелогрпма ппотивоположные стороны попарно равны. а по условию соседние стороны равны, получается что у него все стороны равны. все доказано

Strannik288

Геометрия

4,6(22 оценок)

1) Проще решить эту задачу, представив векторы в координатной форме.

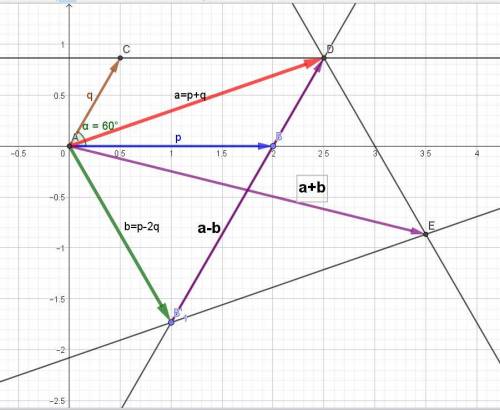
Пусть вектор p по оси Ох, его координаты p(2; 0).

Вектор q повёрнут от вектора р на угол ϕ = (π/3) = 60 градусов.

q(x) = |q|*cos ϕ = 1*(1/2) = 1/2.

q(y) = |q|*sin ϕ = 1*(√3/2) = √3/2.

Далее определяем координаты векторов a и b.

a(x) = p(x) + q(x) = 2 + (1/2) = (5/2).

a(y) = p(y) + q(y) = 0 + (√3/2) = (√3/2).

Вектор a((5/2); (√3/2)), |a| = √((25/4) + (3/4)) = √(28/4) = √7.

Аналогично для вектора b.

b(x) = p(x) - 2q(x) = 2 – 2*(1/2) = 1.

b(y) = p(y) - 2q(y) = 0 - 2(√3/2) = -√3.

Вектор b(1; (-√3)), |b| = √(1 + 3) = √4 = 2.

Теперь определяем координаты векторов как диагоналей параллелограмма, построенного на векторах a и b.

d1 = a + b = ((5/2) + 1; (√3/2) + (-√3)) = ((7/2); (-√3/2)).

d1 = a - b = ((5/2) - 1; (√3/2) – (-√3)) = ((3/2); (3√3/2)).

Находим модули этих векторов, то есть их длины.

|d1| = √((7/2)² + (-√3/2)²) = √((49/4) + (3/4)) = √(52/4) = √13 ≈ 3,6056..

|d2| = √((3/2)² + (3√3/2)²) = √((9/4) + (27/4)) = √(36/4) = √9 = 3.

2) Косинус угла между векторами а и b определяем по формуле

cos ϕ = (a(x)*b(x) + a(y)*b(y))/(√((a(x))² + (b(x))²) * √((a(y))² + (b(y))²) =

= ((5/2)*1 + (√3/2)* (-√3))/( (√((5/2)² + (√3/2)²)*√(1² + (-√3)²) =

= ((5/2) – (3/2))/(√(25/4) + (3/4))*√(1 + 3) =

= 1/(√7*2) = √7/14 ≈ 0,18898.

3) У этой задачи есть два решения.

а) Площадь параллелограмма, построенного на векторах равна модулю векторного произведения этих векторов.

Находим векторное произведение по схеме Саррюса.

I j k| I j

5/2 √3/2 0| 5/2 √3/2

1 -√3 0| 1 -√3 = 0i + 0j – (√3*5/2)k – 0j – 0i - (√3/2)k =

= 0i + 0j - (3√3)k.

Вектор произведения равен (0; 0; (-3√3)).

Площадь S параллелограмма равна:

S = √(0² + 0² + (-3√3)²) = √27 = (3√3) кв. ед.

б) Площадь S параллелограмма, построенного на векторах, равняется произведению длин этих векторов на синус угла, который лежит между ними: S = |a|*|b|*sin ϕ.

Находим синус угла ϕ по формуле

sin ϕ = √(1 - cos² ϕ) = √(1 – (√7/14)²) = √(1 – (7/196)) = √(189/196) = 3√21/14.

S = √7*2*3√21/14 = 3√3 кв. ед.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.