Квадрат и прямоугольник имеет одинаковую площадь-64 см в квадрате. узнай периметр прямоугольника, если его длина в 2 раза больше длины стороны квадрата.

207

251

Посмотреть ответы 3

Ответы на вопрос:

ibg478

Математика

4,8(4 оценок)

площадь квадрата 64, значит его сторона а = 8 см,

8 * 2 = 16 (см) -длина прямоугольника

64: 16 = 4(см) - ширина прямоугольника

(16 + 4)*2 = 40(см) - периметр

rgfheh

Математика

4,4(68 оценок)

8*8=64(см²), 8см-стороны квадрата

8*2=16(см)сторона прямоугольника

64: 16=4(см)другая сторона прямоугольника

р=16*2+4*2=40(см)

ответ: р прямоугольника 40см.

salimova77

Математика

4,6(29 оценок)

Пусть - это сторона, равная 9 см, 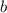- сторона, равная 10 см, - сторона, равная 11 см. Напротив большей стороны лежит больший угол, следовательно, самый большой угол в этом треугольнике, тот, что лежит напротив .

По теореме косинусов:

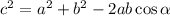
$c^2 = a^2 + b^2 -2ab\cos\alpha$

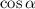$\cos\alpha$ - искомая величина. Выражаем её и вычисляем:

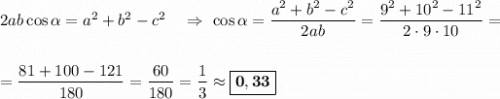
$2ab\cos\alpha = a^2+b^2-c^2\ \ \ \Rightarrow\ \cos\alpha = \dfrac{a^2+b^2-c^2}{2ab} = \dfrac{9^2 + 10^2 - 11^2}{2\cdot 9\cdot 10} =\\\\\\=\dfrac{81+100-121}{180} = \dfrac{60}{180} = \dfrac{1}{3} \approx \boxed{\bf{0,33}}$

Так как самый большой угол данного треугольника имеет положительный косинус, то этот треугольник остроугольный (косинус прямого угла равен нулю, а тупого - отрицателен. Так как у нас косинус самого большого угла в треугольнике положителен, то этот угол является острым).

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.