Тема теорема косинусов 1) стороны треугольника = 5 см , 7см и квадратный корень с 18 найти наибольший кут треугольника . 2)стороны треугольника = 16 см , 18 см и 26 см . найти медиану треугольника , проведенную до его большой стороны

206

320

Посмотреть ответы 2

Ответы на вопрос:

Мариелла17

Геометрия

4,8(13 оценок)

1. δabc: . ab=5 см, bc=7 см, ac=√18 см < a -больший угол δ авс (против большей стороны в треугольнике лежит больший угол). по теореме косинусов: bc²=ab²+ac²-2*ab*ac*cos< a 7²=5²+(√18)²-2*5*√18*сos< a 49-25-18=-10√18*cos< a 6=-10*3*√2*cos< a cos< a=-1/5√2 < a=arccos(-1/(5√2)) < a≈98,13° . 2. δabc: ab=16 см, ac=18 см, bc=26 см ак- медиана, проведенная к большей стороне. из δавк по теореме косинусов: ak²=ab²+(bc/2)²-2*ab*(bc/2)*cos< b. cos< b=? δавс по теореме косинусов: ac²=ab²+bc²-2*ab*bc*cos< b 18²=16²+26²-2*16*26*cos< b 324-256-676=-2*16*26*cos< b -608=-2*16*26*cos< b cos< b=608/(2*16*26) δabk: ak²=16²+13²-2*16*13*608/(2*16*26) ak²=256+169-304 ak²=121 ak=11 см

AnnyMay2629

Геометрия

4,6(54 оценок)

Дано:

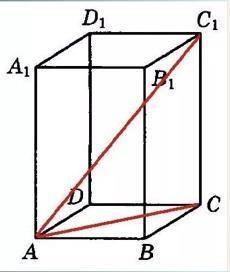
Правильная четырёхугольная призма.

АВ = 4 см.

AC1 = 4√3 см.

Найти:

V - ?

Решение:

"Правильный многоугольник - многоугольник, у которого все углы и стороны равны".

Так как данная призма - правильная, четырёхугольная => основание этой призмы - квадрат.

"Квадрат - геометрическая фигура, у которой все стороны равны".

=> АВ = AD = CD = CB = 4 см.

АС - диагональ квадрата.

d = a√2, где d - диагональ квадрата АС; а - сторона квадрата.

=> АС = 4√2 см.

СС1 = h призмы.

Найдём СС1 (h), по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)

a = √(c² - b²) = √((4√3)² - (4√2)²) = 4 см.

Итак, СС1 = h = 4 см.

V = S основания * h

Основание - квадрат.

S квадрата = а² = 4² = 16 см.

V = 16 * 4 = 64 см³

ответ: 64 см³
Найдите объем правильной четырехугольной призмы, у которой сторона основания равна 4 см, а диагональ

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.