04.02.2022 20:21

Есть ответ 👍

Винни-пух был в гостях у пяточка.уходя, он забыл у него свой воздушный шарик.пятячок заметил это только через 12 минут после ухода винни-пуха и сразу побежал за ним в догонку,чтобы отдать шарик.ему удалось догнать винни довольно быстро,поскольку тот шёл не торопясь,со скоростью 50 м/м,а пятячок бежал быстро со скоростью 200 м/м.запишите на языке.1)какое расстояние винни пух прошёл за 12 минут.2) на какое расстояние пятячок приближался к винни пуху за 1 минуту.3)сколько времени понадобилось пяточку чтобы догнать винни пуха

237

473

Посмотреть ответы 3

Ответы на вопрос:

Кирито7449

Математика

4,5(11 оценок)

1)50*12=600(м)-прошёл винни пух 2)200-50=1509м)-приближался п. к в. за 1 мин 3)600: 150=4(мин)-п. чтобы догнать в.

umnik250

Математика

4,5(69 оценок)

2)200-50- = на 150 в одну минуту 1)12*50=600 метров 3) когда растояни между ними будет равно 0? предположим за время х, тогда 200 * х=12*50+х*50, отсюда 200х-50х=600, то есть 150х=600, значит х=4мин

tinita15

Математика

4,5(16 оценок)

Для начала нужно решить соответствующее линейное однородное дифференциальное уравнение, выполнив замену 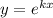$y=e^{kx}$ .

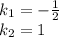
$k_1=-\frac{1}{2}\\ k_2=1$

Общее решение однородного диф. уравнения: 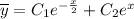$\overline{y}=C_1e^{-\frac{x}{2}}+C_2e^x$ .

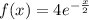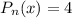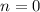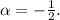Рассмотрим функцию $f(x)=4e^{-\frac{x}{2}}$ . Здесь P_n(x)=4 , где n=0 , $\alpha =-\frac{1}{2}.$ Сравнивая 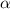$\alpha$ с корнями характеристического уравнения и принимая во внимая, что

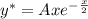
$y^*=Axe^{-\frac{x}{2}}$

Определим первые две производные функции частного решения и подставляем в исходное дифференциальное уравнение одновременно разделив обе части на 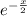$e^{-\frac{x}{2}}$ .

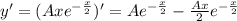
$y'=(Axe^{-\frac{x}{2}})'=Ae^{-\frac{x}{2}}-\frac{Ax}{2}e^{-\frac{x}{2}}$

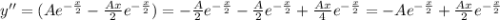
$y''=(Ae^{-\frac{x}{2}}-\frac{Ax}{2}e^{-\frac{x}{2}})=-\frac{A}{2}e^{-\frac{x}{2}}-\frac{A}{2}e^{-\frac{x}{2}}+\frac{Ax}{4}e^{-\frac{x}{2}}=-Ae^{-\frac{x}{2}}+\frac{Ax}{2}e^{-\frac{x}{2}}$

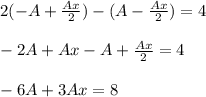
$2(-A+\frac{Ax}{2})-(A-\frac{Ax}{2})=4\\ \\ -2A+Ax-A+\frac{Ax}{2}=4\\ \\ -6A+3Ax=8$

Приравниваем коэффициенты при степенях x

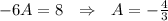
$-6A=8~~\Rightarrow~~ A=-\frac{4}{3}$

Общее решение линейного неоднородного дифференциального уравнения ищем как сумму общего однородного диф. уравнения и частного решения

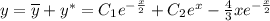
$y=\overline{y}+y^*=C_1e^{-\frac{x}{2}}+C_2e^x-\frac{4}{3}xe^{-\frac{x}{2}}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.