Решите (хватит ответа) 1)боковую сторону трапеции разделили на три равных отрезка и через их концы проведены отрезки параллельные основаниям . найдите длины этих отрезков, если основания трапеции равны 2 и 5. 2)на стороных треугольника abc взяты точки m,n,p так что они делят стороны ab,bc,ca в отношении 1 : 2, считая с вершины a,b,c найти площадь треугольника mnp , если известно что площадь abc равна s 3)площади двух квадратов относятся как 25 : 9. сторона первого на 10 длинее стороны другого . определите сторону меньшего квадрата

254

297

Посмотреть ответы 2

Ответы на вопрос:

JOKER7500

Геометрия

4,5(73 оценок)

1)рассмотрим рисунок этой поделенной на 3 части трапеции. поведя из вершины у меньшего основания прямую, параллельную одной из боковых сторон, получили треугольник и параллелограмм.

каждая из этих фигур разделена на 3 части.

в параллелограмме стороны равны, а части искомых отрезков равны меньшему основанию трапеции. треугольник же делится на подобные треугольники по свойству равенства углов при параллелльных прямых ( которые мы провели при разделении трапеции) и секущей, а угол при вершине этих треугольников - общий. так как боковая сторона разделена на 3 равные части, то отношение сторон этих треугольников 1: 2: 3основание большего треугольника (его боковая сторона=боковая сторона трапеции) равно разности оснований:

5 - 2=3т.к. боковая сторона трапеции разделена на 3 равныечасти, отношение сторон меньшего ( верхнего) треугольника и большего равно 1: 3следовательно, его основание равно ⅓ ·3=1 смотношение второго по величине треугольника и большего равно 2: 3, отсюда его основание равно ⅖·3=2 смтак как длина каждого из проведенных параллелльных отрезков больше оснований треугольников на 2, то: длина искомых отрезков равна: 1 см+2=3 см2см+2=4см2)стороны треугольника mnp относятся к сторонам авс как 1: 3,т.к. каждая сторона δ авс разделена в отношении 1: 2. и эта одна часть - сторона δ mnp, стороне же авс остаются её 3 части. треугольники авс и mnp подобны, так как их сходственные стороны пропорциональны и коэффициент подобия этих треугольниковk=1/3площади подобных фигур относятся, как квадрат их коэффициента подобия, а в этой в отношении (1/3)²=1/9.площадь δ mnp=1/9 площади тр-ка авси равна 1/9 от s или s/93)

площади подобных фигур относятся, как квадрат их коэффициента подобия. т.к. площади квадратов относятся как 25: 9, то коэффициент подобия ( отношение сторон квадратов) равенk=√(25/9)=5/3пусть сторона меньшего квадрата равна х.тогда сторона большего равна х+10

(х+10): х=5: 3по свойству пропорции3(х+10)=5х3х+30=5х2х=30х=15сторона меньшего квадрата равна 15проверка: площадь большего квадрата (15+10)²=625площадь меньшего 15²=225625: 225=25: 9

Ростик22812312

Геометрия

4,7(80 оценок)

ответ: Sбок.пов=27см²

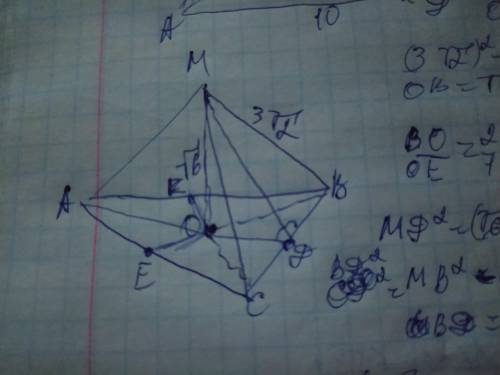
Объяснение: в основании правильной трёхугольной пирамиды лежит равносторонний треугольник. Проведём в нём высоты ДЕК, которые также являются биссектриса и и медианами основания. Отметим точку их пересечения О. Медианы при пересечении делятся в отношении 2: 1, начиная от вершины треугольника. Рассмотрим полученный ∆МОВ. Он прямоугольный и МО и ВО в нём являются катетами а ВМ- гипотенуза. Найдём ОВ по теореме Пифагора:

ВО²=МВ²-МО²=(3√2)²-(√6)²=9×2-6=18-6=12;

ВО=√12=2√3см

Так как ВО/ОЕ=2/1, то ОЕ=ОК=ОД=2√3/2=

=√3см

Также найдём МД в ∆МДО по теореме Пифагора: МД²=МО²+ДО²=(√6)²+(√3)³=

=6+3=9; МД=√9=3см

Теперь найдём сторону ВД в ∆СМВ по теореме Пифагора: ВД²=МВ²-МД²=

=(3√2)²-3²=9×2-9=18-9=9; ВД=√9=3см

Так как ∆СМВ равнобедренный (МВ=МС=3√2), то ВД=СД=3см. Следовательно ВС=3×2=6см

Теперь найдём площадь боковой грани СМВ по формуле:

Sбок.гр=½×BC×МД=½×6×3=9см².

Так как таких граней 3 то:

Sбок.пов=9×3=27см²

В правильной треугольной пирамиде MABC боковое ребро = 3√2 см, а высота пирамиды = √6 см. Найдите пл

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.