Определите отношение радиусов вписанной окружности правильных треугольников, если их площади соответственно равны 9см и 16см.

180

206

Посмотреть ответы 2

Ответы на вопрос:

bogdan975

Геометрия

4,8(85 оценок)

Радиус вписанной окружности правильного треугольника r = , где а - сторона соответствующего треугольника отношение радиусов (т.е. если поделить формулы друг на друга) исходя из этой формулы равно отношению сторон треугольников, т. е. а1/а2 отношение сторон можно найти исходя из площадей. формула площади правильного треугольника s = если поделить формулы площади двух треугольников друг на друга, то получим, что после сокращения останется значит, отношение площадей равно квадрату отношения сторон. отношение площадей равно 16/9. значит, извлекая корень из 16/9, получим соотношение сторон треугольников, равное 4/3. а как мы уже выше выяснили, отношение сторон равно отношению радиусов, то есть 4 к 3 (4: 3 или 4/3). - если записать через отношение большего треугольника к меньшему. а если через отношение меньшего к большему, тогда 3 к 4 (3: 4 или 3/4).

sofisofiyaSofi

Геометрия

4,4(21 оценок)

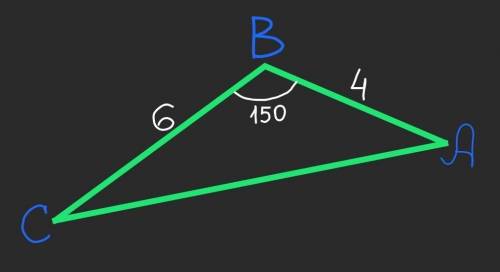
Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.

а=6 см по условию;

с=4 см по условию;

sin(a)=sin(180°–a)

sin(30°)=0,5

Тогда sin(150°)=0,5 так же

Получим:

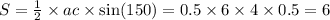
$S = \frac{1}{2} \times ac \times \sin(150) = 0.5 \times 6 \times 4 \times 0.5 = 6$

ответ: 6 см²

Нехай а i c— сторони трикутника, В – кут між ними. Знайдіть площу трикутника, якщо a = 6 см, с = 4 с

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.