Регистрация Спросить otvet5GPT
elezavetkavtoray
25.10.2020 16:46
Алгебра
Есть ответ 👍

Y= lg(9 - 3x) знайти область визначення

184
484
Посмотреть ответы 2

Ответы на вопрос:

kristina05081999
kristina05081999
4,4(58 оценок)
Подлогарифмическое выражение всегда должно быть больше 0: ответ: x∈(-бесконечность; 3)
Света0475
Света0475
4,8(69 оценок)

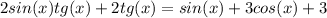
2sin(x)tg(x) + 2tg(x) = sin(x) + 3cos(x) + 3

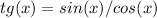
tg(x) = sin(x)/cos(x)

ОДЗ x≠ (π/2) + πn, n∈Z.

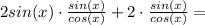
2sin(x)\cdot \frac{sin(x)}{cos(x)} + 2\cdot\frac{sin(x)}{cos(x)} =

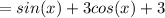
= sin(x) + 3cos(x) + 3

Домножим уравнение на cos(x)≠0,

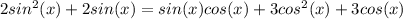
2sin^2(x) + 2sin(x) = sin(x)cos(x) + 3cos^2(x) + 3cos(x)

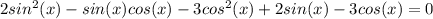
2sin^2(x) - sin(x)cos(x) - 3cos^2(x) + 2sin(x) - 3cos(x) = 0

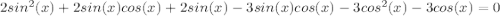
2sin^2(x) + 2sin(x)cos(x) + 2sin(x) - 3sin(x)cos(x)-3cos^2(x)-3cos(x)=0

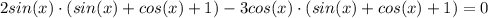
2sin(x)\cdot (sin(x) + cos(x) + 1) - 3cos(x)\cdot (sin(x) + cos(x) + 1) = 0

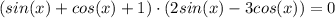
(sin(x) + cos(x) + 1)\cdot (2sin(x) - 3cos(x)) = 0

1) sin(x) + cos(x) + 1 = 0

или

2) sin(x) - 3cos(x) = 0.

Решаем 1)

sin(x) + cos(x) = -1,

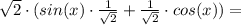
\sqrt{2}\cdot (sin(x)\cdot\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\cdot cos(x))=

= -1

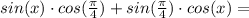
sin(x)\cdot cos(\frac{\pi}{4}) + sin(\frac{\pi}{4})\cdot cos(x) =

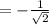
= -\frac{1}{\sqrt{2}}

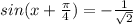
sin(x+\frac{\pi}{4}) = -\frac{1}{\sqrt{2}}

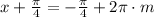
x+\frac{\pi}{4} = -\frac{\pi}{4} + 2\pi\cdot m

или

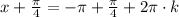
x + \frac{\pi}{4} = -\pi + \frac{\pi}{4} + 2\pi\cdot k

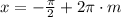
x = -\frac{\pi}{2} + 2\pi\cdot m

эта серия решений не входит в ОДЗ.

или

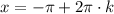
x = -\pi + 2\pi\cdot k

Решаем 2)

sin(x) - 3cos(x) = 0,

sin(x) = 3cos(x),

делим на cos(x)≠0,

sin(x)/cos(x) = 3,

tg(x) = 3,

x = arctg(3) + π·m

ответ. x = -π + 2πk, k∈Z или x=arctg(3) + πm, m∈Z.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS