Алгебра: Решите неравенство методом интервалов (x-1)*(x-2)/(x-3) 0

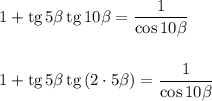
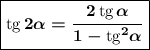
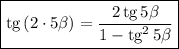
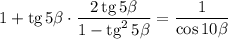
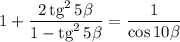
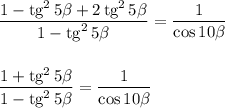
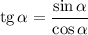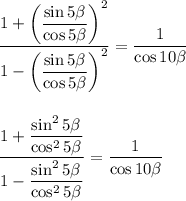
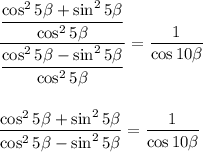
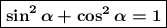
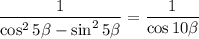
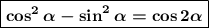
Воспользуемся формулой тангенса двойного угла:Тогда у нас:Заменяем в условии:Выполним умножение:В левой части приводим слагаемые к одному знаменателю:Так как , то:Приводим к одному знаменателю:По основному тригонометрическому тождеству:Тогда в числителе получается:По формуле косинуса двойного угла:Тогда имеем:После преобразований левая и правая части оказались одинаковы, а значит, тождество доказано....

LadaSova

28.10.2021 02:25

Алгебра

Есть ответ 👍

Решите неравенство методом интервалов (x-1)*(x-2)/(x-3)> 0

108

140

Посмотреть ответы 2

Ответы на вопрос:

dmit0

Алгебра

4,8(20 оценок)

Решение смотри на фотографии

neannopad7

Алгебра

4,6(29 оценок)

$1+\text{tg}\,5\beta\,\text{tg}\,10\beta = \dfrac{1}{\cos10\beta}1+\text{tg}\,5\beta\,\text{tg}\left(2\cdot5\beta\right) = \dfrac{1}{\cos10\beta}$

Воспользуемся формулой тангенса двойного угла:

$\boxed{\boldsymbol{\text{tg}\,2\alpha = \dfrac{2\,\text{tg}\,\alpha}{1-\text{tg}^2\alpha}}}$

Тогда у нас:

$\boxed{\text{tg}\left(2\cdot5\beta\right) = \dfrac{2\,\text{tg}\,5\beta}{1-\text{tg}^2\,5\beta}}$

Заменяем в условии:

$1+\text{tg}\,5\beta\cdot\dfrac{2\,\text{tg}\,5\beta}{1-\text{tg}^2\,5\beta} = \dfrac{1}{\cos10\beta}$

Выполним умножение:

$1+\dfrac{2\,\text{tg}^2\,5\beta}{1-\text{tg}^2\,5\beta} = \dfrac{1}{\cos10\beta}$

В левой части приводим слагаемые к одному знаменателю:

$\dfrac{1-\text{tg}^2\,5\beta + 2\,\text{tg}^2\,5\beta}{1-\text{tg}^2\,5\beta} = \dfrac{1}{\cos10\beta}dfrac{1+\text{tg}^2\,5\beta}{1-\text{tg}^2\,5\beta} = \dfrac{1}{\cos10\beta}$

Так как $\text{tg}\,\alpha = \dfrac{\sin\alpha}{\cos\alpha}$ , то:

$\dfrac{1 + \left(\dfrac{\sin5\beta}{\cos5\beta}\right)^2}{1 - \left(\dfrac{\sin5\beta}{\cos5\beta}\right)^2} = \dfrac{1}{\cos10\beta}dfrac{1+\dfrac{\sin^25\beta}{\cos^25\beta}}{1-\dfrac{\sin^25\beta}{\cos^25\beta}} = \dfrac{1}{\cos10\beta}$

Приводим к одному знаменателю:

$\dfrac{\dfrac{\cos^25\beta + \sin^25\beta}{\cos^25\beta}}{\dfrac{\cos^25\beta - \sin^25\beta}{\cos^25\beta}}} = \dfrac{1}{\cos10\beta}dfrac{\cos^25\beta + \sin^25\beta}{\cos^25\beta - \sin^25\beta} = \dfrac{1}{\cos10\beta}$

По основному тригонометрическому тождеству:

$\boxed{\boldsymbol{\sin^2\alpha+\cos^2\alpha = 1}}$

Тогда в числителе получается:

$\dfrac{1}{\cos^25\beta-\sin^25\beta} = \dfrac{1}{\cos10\beta}$

По формуле косинуса двойного угла:

$\boxed{\boldsymbol{\cos^2\alpha -\sin^2\alpha = \cos2\alpha}}$

Тогда имеем:

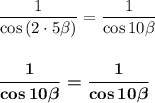
$\dfrac{1}{\cos\left(2\cdot5\beta\right)} = \dfrac{1}{\cos10\beta}boldsymbol{\dfrac{1}{\cos10\beta} = \dfrac{1}{\cos10\beta}}$

После преобразований левая и правая части оказались одинаковы, а значит, тождество доказано.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.