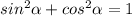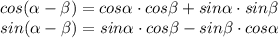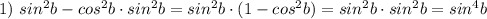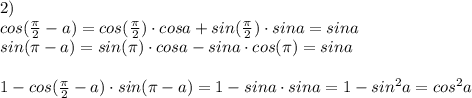Регистрация Спросить otvet5GPT
elizavetaelise1
24.03.2023 14:13
Алгебра
Есть ответ 👍

Найдите наибольшее и наименьшее значение функции y=x/4+1/(x-5) на промежутке [6; 8]

171
386
Посмотреть ответы 2

Ответы на вопрос:

iwcukq
iwcukq
4,4(26 оценок)
Для этого найдем производную данной функции.  y' = 1/4   - 1/(x-5)² приводим к общему знаменателю: y' = ((x - 5)²   - 4) / (4(x-5)²) y' = (x² - 10x + 21) / (4(x-5)²) найдем нули производной: x² - 10x + 21 = 0 d = 100 - 84 = 4² x₁ = (10 - 4) / 2= 3  x₂ = (10 + 4) / 2= 7 нанесём на числовую прямую, не забыв про число 5 из знаменателя: > подставим значения из промежутков в производную и посмотрим знаки производной при этих числах:   +      -      -     +   > точка минимума - точка, где производная меняет знак с минуса на плюс. точка максимума  - точка, где производная меняет знак с плюса  на минус. точка максимума - 3. но 3 не входит в оо. точка минимума - 7.  значит, посчитаем значение функции в точках 6, 7 и 8. f(6) = 2.5 f(7) =    2.25 f(8) = 7/3 ответ: наибольшее значение - 2.5. наименьшее значение - 2.25.
keksvanil
keksvanil
4,4(82 оценок)

Объяснение:

Нам потребуется:

основное тригонометрическое тождество:

sin^2\alpha+cos^2\alpha=1

формулы косинуса и синуса разности:

cos(\alpha-\beta)=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\\sin(\alpha-\beta)=sin\alpha\cdot cos\beta - sin\beta\cdot cos\alpha

1) $ $sin^2 b-cos^2 b\cdot sin^2 b= sin^2b\cdot (1-cos^2b)=sin^2b\cdot sin^2b=sin^4b

2) \\cos(\frac{\pi}{2}-a)=cos(\frac{\pi}{2})\cdot cosa+sin(\frac{\pi}{2})\cdot sina=sina\\sin(\pi-a)=sin(\pi)\cdot cosa-sina\cdot cos(\pi)=sina\\\\1-cos(\frac{\pi}{2}-a)\cdot sin(\pi-a)=1-sina\cdot sina=1-sin^2a=cos^2a

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS