Регистрация Спросить otvet5GPT
Khajiit999
31.01.2020 09:47
Математика
Есть ответ 👍

Монету подбрасывают 4 раза. найти вероятность, что 3-й и 4-й раз выпали "решки", если известно, что "орел" выпадал не более 2 раз. большое за решение: )

222
377
Посмотреть ответы 2

Ответы на вопрос:

kate2224
kate2224
4,4(82 оценок)
Странное задение. либо тут лишние данные, либо просто хотят запутать. вероятность выпадения решки при броске всегда равна 0,5 и не зависит от того, что и сколько раз выпадало раньше. поэтому вероятность двух подряд решек равна 0,5*0,5=0,25 вне зависимости от того какие это по счёту броски и  сколько орлов или решек было до этого. вроде так как-то.
настя7096
настя7096
4,4(28 оценок)

-8π , -9π , -49π/6 , -53π/6

Пошаговое объяснение:

а)

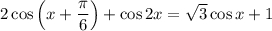
\displaystyle 2\cos \left ( x+\frac{\pi }{6} \right )+\cos2x=\sqrt{3}\cos x+1

Распишем cos(x+π/6) по формуле сложения аргументов: cos(α+β) = cosαcosβ - sinαsinβ

То есть:

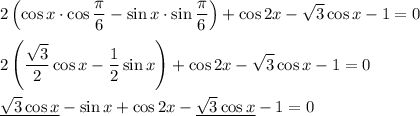
\displaystyle 2\left ( \cos x\cdot \cos \frac{\pi }{6} -\sin x \cdot \sin \frac{\pi}{6} \right )+\cos2x -\sqrt{3}\cos x -1=02\left (\frac{\sqrt{3} }{2} \cos x - \frac{1}{2}\sin x \right )+\cos2x-\sqrt{3} \cos x -1 =0 \underline{\sqrt{3} \cos x }- \sin x+\cos 2x-\underline{\sqrt{3}\cos x} -1 =0

Заменим cos2x = 1-2sin²x , тогда:

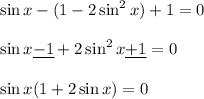
\displaystyle \sin x -(1-2\sin^2x)+1=0 \sin x\underline{ -1}+2\sin ^2x\underline{+1}=0 \sin x(1+2\sin x)=0

Получаем совокупность двух уравнений , причем , для удобства запишем корни не в общем виде:

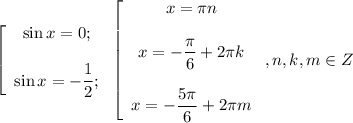
\left [ \begin{array}{ccc} \sin x = 0; \displaystyle \sin x = -\frac{1}{2} ;\end{array}\right \left [ \begin{array}{ccc} x=\pi n \displaystyle x=-\frac{\pi}{6} +2\pi kdisplaystyle x=-\frac{5\pi}{6}+2\pi m \end{array}\right,n,k,m\in Z

б)

Сделаем отбор корней с двойного неравенства:

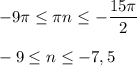
\displaystyle -9\pi \leq \pi n\leq -\frac{15\pi}{2} -9\leq n\leq -7,5

Так как n∈Z , то нам подходит n = -9 , -8 .

Подставляем:

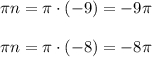
\pi n = \pi \cdot (-9)=-9\pipi n = \pi \cdot (-8) = -8\pi

Уже два корня на указанном отрезке мы нашли , ищем дальше.

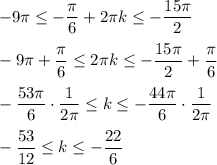
\displaystyle -9\pi \leq -\frac{\pi}{6}+2\pi k\leq -\frac{15\pi}{2}-9\pi +\frac{\pi }{6} \leq 2\pi k \leq -\frac{15\pi}{2}+\frac{\pi}{6} -\frac{53\pi }{6} \cdot \frac{1}{2\pi} \leq k\leq -\frac{44\pi}{6} \cdot \frac{1}{2\pi } -\frac{53}{12} \leq k\leq -\frac{22}{6}

Нас устраивает k = -4 , подставим:

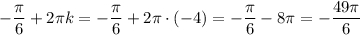
\displaystyle -\frac{\pi }{6} +2\pi k = -\frac{\pi }{6}+2\pi \cdot (-4)=-\frac{\pi}{6}-8\pi = -\frac{49\pi }{6}

Осталось немного , ищем дальше:

\displaystyle -9\pi \leq -\frac{5\pi}{6}+2\pi m\leq -\frac{15\pi}{2}-9\pi +\frac{5\pi }{6} \leq 2\pi m \leq -\frac{15\pi}{2}+\frac{5\pi}{6} -\frac{49\pi }{6} \cdot \frac{1}{2\pi} \leq m \leq -\frac{40\pi}{6} \cdot \frac{1}{2\pi } -\frac{49}{12} \leq m \leq -\frac{10}{3}

Нам подходит m = -4 , следовательно:

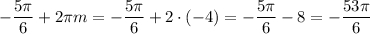
\displaystyle -\frac{5\pi}{6}+2\pi m = -\frac{5\pi}{6}+2\cdot (-4)=-\frac{5\pi }{6} -8= -\frac{53\pi}{6}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS