Стороны основания прямого параллелепипеда равны 1 см и 3 см, а синус угла между ними `sqrt5 /3`. найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно `sqrt(14)` см.

142

259

Посмотреть ответы 2

Ответы на вопрос:

LipskiyTimur

Геометрия

4,7(21 оценок)

Sin a = √5/3; cos^2 a = 1 - sin^2 a = 1 - 5/9 = 4/9; cos a = √(4/9) = 2/3 a = arccos(2/3) ~ 48 градусов, это острый угол. cos b = cos(180 - a) = -cos a = -2/3 по теореме косинусов в треугольнике авс в основании d^2 = a^2 + b^2 - 2ab*cos b здесь d - это диагональ основания, a и b - стороны основания. d^2 = 1^2 + 3^2 - 2*1*3*(-2/3) = 1 + 9 + 4 = 14 d = √14 - это длина диагонали основания. h = √14 - боковое ребро. все это нарисовано на левом рисунке. диагональ основания, боковое ребро и большая диагональ пар-педа образуют прямоугольный треугольник. так как d = h, то этот прямоугольный треугольник к тому же равнобедренный. угол между большой диагональю ac' и диагональю основания ас = 45 гр. это нарисовано на правом рисунке.

chizhikovilya

Геометрия

4,5(12 оценок)

б) 4/5 по теореме Пифагора находим гипотенузу

и пишем отношение большего катета к ней

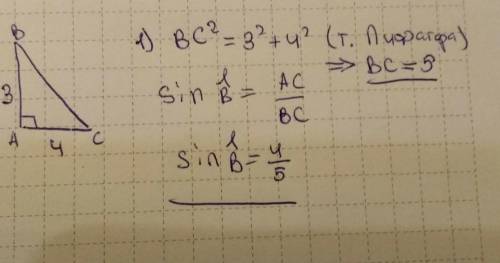
Катети прямокутного трикутника 3 см і 4 см. Знайдіть синус кута протилежного більшому катету. Вариан

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.