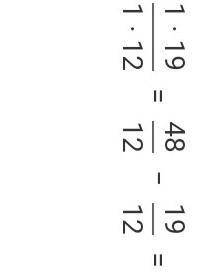Найдите найбольшие значение функции на отрезке [-13; -3.5] y=x^3+10x^2+25x+11

103

165

Посмотреть ответы 2

Ответы на вопрос:

asdfdsf01oziqid

Математика

4,7(58 оценок)

Найдем производную y'=(x^3+10x^2+25x+11)'=3x^2+20x+25 приравнивай производную к нолю и находим точки 3x^2+20x+25=0 д=400-4*3*25=400-300=100 х1=(-20-10)/(6)=-30/6=-5 х2=(-20+10)/6=-10/6=-5/3=-1 целая 2/3 получили две точки, которые делят ось ох на три промежутка: 1=(- беск; --5), 2=(-5; -1 целая 2/3), 3=(-1 целая 2/3; беск).; обязательно нарисовать, показав эти интервалы и знак производной определим знак производной на этих интервалах 1=(- беск; --5): + -6: 3(-6)^2+20*(-6)+25=3*36-120+25=108-120+25=13 2=(-5; -1 целая 2/3), - -3: 3(-3)^2+20(-3)+25=3*9-60+25=27-60+25=-8 3=(-1 целая 2/3; беск).; + 0: 3*0^2+20*0+25=0+0+25=25 видим что точка х=-5 является минимум функции,а точка х=-1 целая 2/3 максимум так как точка х=-1 целая 2\3 не входит в интервал, на котором определяем наибольшее и наименьшее значение функции то про нее забудем подставим теперь полученные точки и края интервала в функцию y(-13)=(-13)^3+10*(-13)^2+25*(-13)+11=-2197+1690-325+11=-821 y(-5)=(-5)^3+10*(-5)^2+25*(-5)+11=-125+250-125+11=11 y(-3,5)=(-3,5)^3+10*(-3,5)^2+25*(3,5)+11=-42,875+122,5-87,5+11=3,125видим что минимум функции на интервале [-13; -3.5]=у(-13)=-821,а максимум на этом же интервале-у(-5)=11 ответ у мин на интервале [-13; -3.5]=у(-13)=-821, у макс на интервале [-13; -3.5]=у(-5)=11

arada1

Математика

4,4(56 оценок)

Пошаговое объяснение:

как-то так..........

Как решить 4-1целое 7 числитель 12 знаминатель

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.