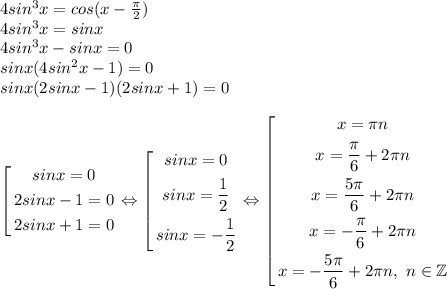Регистрация Спросить otvet5GPT
alinasastun0
21.05.2020 22:29
Математика
Есть ответ 👍

Теория вероятностей и статистика напишите именно решение: в партии из 15 деталей 3 бракованных. покупатель приобрел 5 деталей. найдите вероятность того, что среди них: - есть хотя бы одна бракованная - 3 бракованные детали - 2 бракованные детали сами ответы есть в конце учебника, но решение не могу подобрать. с решением .

242
433
Посмотреть ответы 2

Ответы на вопрос:

Aryyke08
Aryyke08
4,7(36 оценок)
Обозначение:   c из n  по m = n! /[m! *(n - m)! ] - число сочетаний из n  по m (не могу найти здесь мощного матредактора, поэтому так обозначил). 1) событие а  есть хотя бы одна бракованная противоположное  событие _а (не а) - нет ни одной бракованной , т.е. все стандартные.   (ст = 15-3=12 - число стандартных) n =  с из 15 по 5 - число всех элементарных исходов m = с из 12 по 5 - число благоприятствующих событию _а исходов р(_а) = m/n  = [с из 12 по 5]/[с из 15 по 5] р(а) = 1 - р(_а) 3) m = [с из 3 по 2] * [с из 12 по 3]  2 бракованные из 3-х бракованных можно выбрать [с из 3 по 2] способами но к каждому из этих способов можно добавить 3 стандартных из 12-ти стандартных [с из 12 по 3], т.е. перемножаем основное комбинаторное  правило умножения 2) m = [с из 3 по 3]*[с из 12 по 2] - аналогично советую посмотреть  в.е. гмурман "теория вероятностей и статистика" глава 1  § примеры непосредственного вычисления вероятностей, пример 4 - это стандартная . рекомендую также найти гмурман "руководство к решению по теории вероятностей и . статистике"
yana8889
yana8889
4,5(95 оценок)

-\pi; \ -\frac{5\pi}{6}; \ -\frac{\pi}{6}; \ 0; \ \frac{\pi}{6}; \ \frac{5\pi}{6}; \ \pi.

Пошаговое объяснение:

4sin^3x=cos(x-\frac{\pi}{2}) \\ 4sin^3x=sinx \\ 4sin^3x-sinx=0 \\ sinx(4sin^2x-1)=0 \\ sinx(2sinx-1)(2sinx+1)=0 \\ \\ \left[ \begin{gathered} sinx=0\\ 2sinx-1=0 \\ 2sinx+1=0\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} sinx=0\\ sinx=\frac{1}{2} \\ sinx=-\frac{1}{2}\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}x=\pi n\\ x=\frac{\pi}{6}+2\pi n \\ x=\frac{5\pi}{6}+2\pi n \\ x=-\frac{\pi}{6}+2\pi n \\ x=-\frac{5\pi}{6}+2\pi n, \ n\in \mathbb{Z} \end{gathered} \right.

Отрезку [-π;π] принадлежат корни:

-\pi; \ -\frac{5\pi}{6}; \ -\frac{\pi}{6}; \ 0; \ \frac{\pi}{6}; \ \frac{5\pi}{6}; \ \pi.


Найти сумму таких корней уравнения 4sin³x=cos(x-π/2), которые принадлежат отрезку -π, π

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS