Регистрация Спросить otvet5GPT
ashirova1209
20.07.2020 08:50
Алгебра
Есть ответ 👍

Срешением, не сходиться с ответом 2cos2a , если sin^2a=-0,7 а-это альфа

265
375
Посмотреть ответы 1

Ответы на вопрос:

375196albert
375196albert
4,4(19 оценок)

(см. объяснение)

Объяснение:

Попробуем доказать равенство:

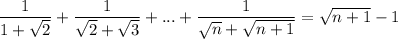
\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{n+1}-1

Применим метод математической индукции.

Докажем базу индукции для 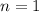n=1:

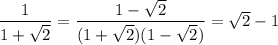\dfrac{1}{1+\sqrt{2}}=\dfrac{1-\sqrt{2}}{(1+\sqrt{2})(1-\sqrt{2})}=\sqrt{2}-1, верно.

Докажем переход:

Предположим, что для 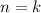n=k выполнено:

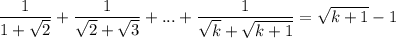
\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{k}+\sqrt{k+1}}=\sqrt{k+1}-1

Тогда для 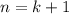n=k+1 согласно предположению:

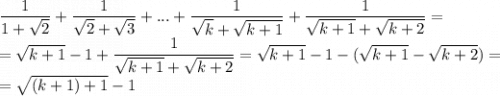
\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{k}+\sqrt{k+1}}+\dfrac{1}{\sqrt{k+1}+\sqrt{k+2}}=\\=\sqrt{k+1}-1+\dfrac{1}{\sqrt{k+1}+\sqrt{k+2}}=\sqrt{k+1}-1-(\sqrt{k+1}-\sqrt{k+2})=\\=\sqrt{(k+1)+1}-1

Значит по принципу математической индукции равенство выполнено для всякого 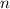n.

Наконец, получили, что:

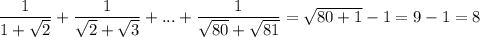
\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{80}+\sqrt{81}}=\sqrt{80+1}-1=9-1=8

Из данных рассуждений заключаем, что правильный ответ указан под буквой Г.

Задание выполнено!

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS