Регистрация Спросить otvet5GPT
Djamila1108
24.03.2022 08:13
Математика
Есть ответ 👍

На изготовление цепочки ювелир израсходовал одну тысячную долю килограмма золота . сколько золота нужно для изготовления пяти таких же цепочек

266
360
Посмотреть ответы 2

Ответы на вопрос:

jutyra
jutyra
4,4(54 оценок)
Одна тысячная доля килограмма - это 1 грамм следовательно, 1 *5 = 5 г золота нужно для изготовления цепочек
agayevaaysu
agayevaaysu
4,6(38 оценок)

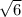
\sqrt{6}

Пошаговое объяснение:

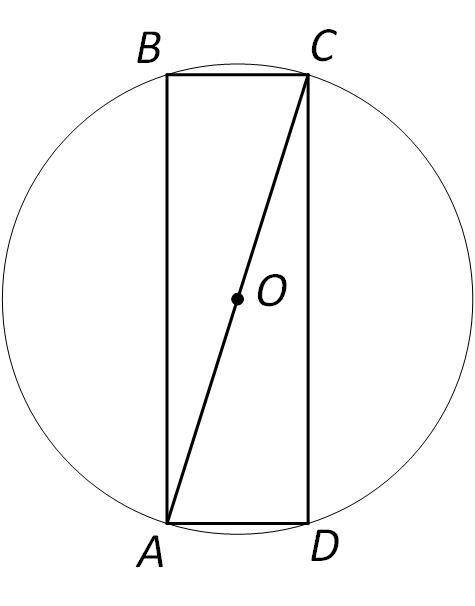
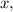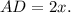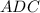
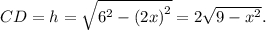
Рассмотрим осевое сечение. Пусть радиус окружности основания цилиндра равен x, тогда AD = 2x. Из теоремы Пифагора для прямоугольного треугольника ADCCD = h = \sqrt {{6^2} - {{(2x)}^2}} = 2\sqrt {9 - {x^2}}.

Объем цилиндра V = Sh = 2\pi {x^2}\sqrt {9 - {x^2}} .

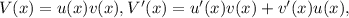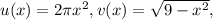
Найдем производную V(x) = u(x)v(x), V'(x) = u'(x)v(x) + v'(x)u(x), где u(x) = 2\pi {x^2}, v(x) = \sqrt {9 - {x^2}} ,v — сложная функция:

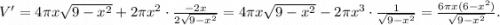
V' = 4\pi x\sqrt {9 - {x^2}} + 2\pi {x^2} \cdot \frac{{ - 2x}}{{2\sqrt {9 - {x^2}} }} = 4\pi x\sqrt {9 - {x^2}} - 2\pi {x^3} \cdot \frac{1}{{\sqrt {9 - {x^2}} }} = \frac{{6\pi x(6 - {x^2})}}{{\sqrt {9 - {x^2}} }}.

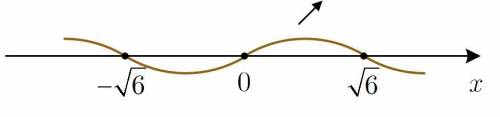
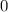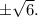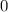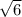Найдем максимум этой функции. Нули производной — числа 0 и  \pm \sqrt 6 . С метода интервалов видим, что функция возрастает от 0 до \sqrt 6  и убывает после 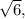\sqrt 6 , таким образом 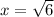x = \sqrt 6  — точка ее максимума.


Найдите радиус основания цилиндра наибольшего объема, который можно вписать в шар радиуса 6.
Найдите радиус основания цилиндра наибольшего объема, который можно вписать в шар радиуса 6.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS